Exapmle: Factoring a Polynomial
![]()
and you’d have to guess again. This guess-and-check method is looooooong and tedious, at best. In fact, this particular quadratic is prime, so you could guess and check all day long and it would never factor.
If you’re in pre-calculus and your teacher is using the guess-and-check method of factoring, which just isn’t working for you, you’ve come to the right section. The following procedure, called the FOIL method of factoring (sometimes called the British Method), always works for factoring trinomials and is a very helpful tool if you can’t wrap your brain around guess-and-check. When the FOIL method fails, you know for certain the given quadratic is prime.
The FOIL method of factoring calls for you to follow the steps required to FOIL binomials, only backwards. Remember that when you FOIL, you multiply the First, Outside, Inside, and Last terms together. Then you combine any like terms, which usually come from the multiplication of the Outer and Inner terms.
For example, to factor
![]()
follow these steps:
-
Check for the GCF first.
The expression
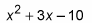
won’t have GCF when you break it down and look at it, according to the steps in the last section. The breakdown looks like this:
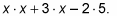
No factors that are common to each term, so there is no GCF. That means you get to move onto the next step.
-
Multiply the quadratic term and the constant term.
Be careful of the signs when you do this. In this example, the quadratic term is
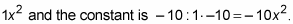
-
Write down all the factors of the result, in pairs.

-
–1x and 10x
-
1x and –10x
-
–2x and 5x
-
2x and –5x
-
-
From this list, find the pair that adds to produce the coefficient of the linear term.
You want the pair whose sum is +3x. For this problem, the answer is –2x and 5x because

-
Break up the linear term into two terms, using the numbers from Step 4 as the coefficients.
Written out, you now have
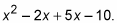
It makes life easier in the long run if you always arrange the linear term with the smallest coefficient first. That’s why you put the –2x in front of the +5x.
-
Group the four terms into two sets of two.
Always put a plus sign between the two sets:
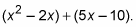
-
Find the GCF for each set and factor it out.
Look at the first two terms. What do they share in common? An x. If you factor out the x, you have x(x – 2). Now, look at the second two terms. They share a 5. If you factor out the 5, you have 5(x – 2). The polynomial is now written as x(x – 2) + 5(x – 2).
-
Find the GCF of the two new terms.
Do you see the (x – 2) in both terms? They’re underlined here: x(x – 2) + 5(x – 2). That’s a GCF because it appears in both terms (if you factor using this method, the last step should always look like this). Factor out the GCF from both terms (it’s always the expression inside the parentheses) to the front; you get (x – 2)( ). When you factor it out, the terms that aren’t the GCF are left inside the new parentheses. In this case, you get (x – 2)(x + 5). The (x + 5) is the leftover from taking away the GCF.
…and Math Tutoring offers math tutoring in the north county of San Diego (Oceanside, Vista, Carlsbad, San Marcos…) and EVERYWHERE online. Call us at 818-970-4800 or CLICK HERE.
